Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
- Интервал — это часть прямой, ограниченная двумя точками. Но эти точки не принадлежат интервалу. Интервал обозначается круглыми скобками: (1; 5),(−7; 3),(11; 25) и т.д.;
- Отрезок — это тоже часть прямой, ограниченная двумя точками. Однако эти точки тоже являются частью отрезка. Отрезки обозначаются квадратными скобками: ,, и т.д.
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
![]()
На этом рисунке отмечен отрезок и интервал (9; 11)
Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
Отмечаем полученные корни на координатной оси:
![]()
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
Отмечаем полученные корни на координатной оси:
![]()
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
- В строгих неравенствах нас не интересуют концы отрезка, поэтому они отмечаются выколотыми точками. Такие точки никогда не входят в ответ, о чем говорят круглые скобки на первом ответе: ∈ (−∞; −3) ∪ (5; +∞);
- И наоборот, в нестрогих неравенствах концы отрезка входят в ответ. На графике они отмечаются закрашенными точками, а в ответе указываются квадратными скобками: ∈ (−∞; −3] ∪ [5; +∞).
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.

В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство \(\frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0\).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
\(\frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = \frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. \)
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ .
Пример 3. Решить неравенство \(\frac{1}{х^2} ≥ \frac{1}{х+2}\)
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
\(\frac{1}{х^2} — \frac{1}{х+2} ≥ 0\).
Приведем к общему знаменателю:
\(\frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0\).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
\(\frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0\).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
\(\frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = \frac{9 + 3 — 2}{9 * (-1)} = \frac{10}{-9}\)
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U .
Давайте подведем итог. Для чего мы это изучили?Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс. Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Знаки и разметка, регулирующие скоростной режим
Самым наглядным способом регулирования скоростного режима являются дорожные знаки и разметка. Подобные варианты весьма наглядно ограничивают максимальную и минимальную скорость движения транспортных средств.
1. Знак «Ограничение максимальной скорости» (3.24)
Запрещающий знак «Ограничение максимальной скорости» (3.24) – самый популярный на дороге. В зоне действия знака водителям запрещается двигаться со скоростью, превышающей величину, указанную на знаке.
Кстати, по совместительству это еще и самый любимый гаишниками знак. Очень часто в зоне действия знака, ограничивающего скоростной режим на дороге, можно встретить либо стационарный, либо переносной радар. А иногда и сами инспекторы ДПС могут располагаться на таких участках.
Парадоксально, но многие водители видят в знаке «Ограничение максимальной скорости» своего врага. Это неверно. Знак, ограничивающий скорость движения, стоит не напрасно: скорее всего, он установлен перед каким-то опасным участком дороги, где водителю следует принудительно снизить скорость для обеспечения максимальной безопасности.
Например, при приближении к пешеходному переходу…
или к месту частого появления детей…
или к искусственной неровности…
или к участку дорожных ремонтных работ…
Именно поэтому водитель должен расценивать указанный знак в качестве своего союзника и советника, стремящегося уберечь его от несчастного случая. Правда, иногда сотрудники ДПС могут с помощью знака создавать «ловушки» — необоснованные ситуацией требования снижения скорости.
Но последний пример – это все-таки исключение. Давайте мыслить позитивно!
2. Знак «Ограничение минимальной скорости» (4.6)
Существуют такие участки дорог, на которых целесообразно было бы регламентировать не максимальную, а минимальную скорость движения. Например, для предотвращения пробок или заторов. С этой целью ПДД применяется специальный предписывающий знак – «Ограничение минимальной скорости».
И чаще всего такое ограничение распространяется на конкретную полосу движения. Это требование оптимизирует процесс движения и делает его более эффективным.
3. Знак «Начало полосы» (5.15.3)
Появление новой полосы для движения (особенно на подъеме), как правило, снабжается знаком особых предписаний – «Начало полосы».
Как видно, в поле знака расположены знаки, ограничивающие минимальную скорость. Поэтому водитель обязан следовать требованиям знака при выборе скоростного режима при движении по конкретной полосе.
4. Знак «Зона с ограничением максимальной скорости» (5.31)
Еще один знак особых предписаний запрещает водителю двигаться с превышением заданного скоростного ограничения.
Такое ограничение действует на обе стороны дороги и распространяется исключительно до отбойного знака – «Конец зоны с ограничением максимальной скорости» (5.32).
5. Знак «Общие ограничения максимальной скорости» (6.1)
Данный информационный знак устанавливается на КПП (контрольно-пропускных пунктах) при въезде на территорию нашей страны.
Знак ничего и никого не ограничивает; он просто информирует об общих принципах ограничения скоростного режима, действующего в Российской Федерации.
6. Знак «Рекомендуемая скорость» (6.2)
Подавляющее большинство водителей незаслуженно игнорируют знак «Рекомендуемая скорость». Они мыслят таким образом: знак просто рекомендует придерживаться указанного скоростного режима, но это рекомендация не носит какого-то обязательного характера.
А давайте взглянем на установку знака по-иному. Почему он установлен? Очевидно, это связано с какой-то опасностью для движения. А теперь главный вопрос: «Стоит ли водителю игнорировать факт опасности на дороге?».
Вопрос риторический!
7. Горизонтальная разметка 1.24.2, дублирующая дорожный знак 3.24
Ограничение максимального скоростного режима, установленного соответствующим знаком, может быть продублировано разметкой.
В случае, когда требования знака и разметки противоречат друг другу, водитель должен следовать указаниям знака.
Подведем предварительный итог. Указанные способы регулирования скоростного режима – весьма наглядны и, следовательно, понятны.
Однако, помимо рассмотренных знаков и разметки, в Правилах существует специальный 10 раздел, регламентирующий скоростные ограничения на дорогах России.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Система уравнений с объединяющими значками может раскрываться с помощью фигурной конфигурации{{. Это характеризует объединение неравенства или уравнений. Пример: {x2−1=0x2+x−2=0x2−1=0x2+x-2=0 или неравенства с несколькими переменными {x2−y>03x+2y≤3, cos x12 (x+π3)=02×2−4≥5×2-y>03x+2y≤3, cos x12x+π3=02×2−4≥5.
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.
Кусочная функция изображается одиночной { скобкой, имеющей формулы, обусловливающие функцию, содержащие определенные промежутки. Пример:|x|={x, x≥0−x, x<0x=x, x≥0-x, x<0.
Для изображения координатных точек в виде промежутков, применяются круглые скобки. Они располагаются на координатной прямой, а также в прямоугольной системе или n-пространстве.
Запись двух координат А (1)А (2) означает, что т. АА имеет координату со значением 12, тогда Q (c, d, e) Q (c, d, e) свидетельствует о том, что т. QQ содержит координаты x, y, zx, y, z.
Множества задаются через перечисление элементов, входящих в эту область с помощью фигурных скобок, где участвующие элементы перечисляются через запятую. Пример: А={5, 6, 7, 8}А={5, 6, 7, 8}.
Примеры решений
Когда в скобки заключают выражение, содержащее круглые и квадратные скобки, пользуются фигурными знаками {}. Вычисление по таким формулам осуществляется в особом порядке: сначала считают внутри всех круглых скобок в определенной последовательности. Затем — внутри всех квадратных и фигурных.
Например, расчет предполагает поэтапное действие. Выражение последовательно 5 — 3 + 2 = 4. Если сначала сложить 3+2, затем отнять от 5−5 получится 0. Для указания правильной последовательности применяют скобки.
(5−2)+3 = 3+3 = 6.
7 — (2+2) = 7−4 = 3.
+(6−4)= + 2= 11+2= 13.
Парные знаки не ставятся, если сложение и вычитание исполняются в указанной последовательности. Также когда внутри происходят операции умножения или деления.
По правилам сначала выполняются операции с цифрами в скобочках, а умножение или деление производятся в порядке их следования, ранее, чем сложение и вычитание. Исполняются остальные действия, а умножение и деление осуществляются в порядке их следования.
При использовании квадратных или фигурных знаков в начале вычисления начинаются внутри круглых скобочек, далее — внутри всех квадратных и фигурных. Оставшиеся действия происходят в последнюю очередь. Обобщающие знаки — скобки важны и незаменимы в математических расчетах для правильного вычисления.
Знаки дополнительной информации (таблички)
Знаки дополнительной информации иначе называются табличками. Они всегда уточняют или дополняют требование какого-либо знака из другой группы.
Применяться отдельно от знака и устанавливаться самостоятельно таблички не могут (за исключением табличек 8.15 и 8.23, которые применяются не только со знаками, но и со светофорами).
С одним дорожным знаком допускается применение не более трех табличек.
Все таблички имеют форму прямоугольника (таблички 8.1.2 и 8.13 — форму квадрата) и, за исключением табличек 8.4.8, 8.5.1, 8.19 и 8.22.1-8.22.3, представляют собой черное изображение на белом фоне.
Предупреждающие знаки
Большинство знаков этой группы имеют треугольную форму, белый фон, красную кайму и черное изображение
Такие знаки всегда устанавливаются заблаговременно до начала опасного участка дороги, чтобы водитель успел принять меры предосторожности
Расстояние от знака до начала опасного участка, о котором предупреждает данный знак, составляет:
- в населенных пунктах — 50-100 метров;
- на загородных дорогах — 150-300 метров.
Допускается установка треугольных знаков и на ином расстоянии, однако при этом под знаком должна находиться табличка «Расстояние до объекта» 8.1.1.
Знаки этой группы, которые имеют иную форму (в виде прямоугольника или крестика), устанавливаются по другим правилам.
Знаки, которые предупреждают водителя о наиболее серьезных опасностях, а именно 1.1, 1.2, 1.9, 1.10, 1.23, 1.25 повторяются вне населенных пунктов. Второй знак ставят не менее чем за 50 м до начала опасного участка дороги.
Кроме того, знаки 1.23 и 1.25 повторяются в населенных пунктах непосредственно в начале опасного участка.
Ниже представлены все предупреждающие знаки. Наведя на знак курсором мыши, вы можете прочитать его название, а щелкнув — увидите описание знака. Для того чтобы успешно справиться с изучением дорожных знаков, вы должны прочитать подробные пояснения к каждому из них.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
Например, выражение $2+3cdot 2$ не равносильно выражению $(2+3)cdot 2$. Для первого выражения сначала вычисляется произведение, а затем сумма, для второго же выражения сначала вычисляется сумма, так как она стоит в скобках, и лишь затем произведение.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Готовые работы на аналогичную тему
Второе применение.
Скобками выделяют отрицательные числа в выражениях для того чтобы избежать путаницы. Например, выражение $(-5) cdot 2 + (3 cdot 12)$. Однако, если отрицательное число стоит в выражении на первом месте, оно может и не выделяться скобками.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Круглыми скобками обозначаются отрезки, границы которых не включены интервал. Интервал с круглыми скобками вида $(-a;+a)$ можно иначе записать как строгое неравенство вида $-a$
Пятое применение.
Скобки также используются при необходимости записи зависимости какой- либо функции от аргумента, например, $f(x)=5x+3$.
Пятое применение.
С помощью скобок записываются координаты точек, например, , запись «точка, с координатами $(1; 2)$» обозначает, что по оси абсцисс координата точки равна единице, а по оси ординат — двум.
Что такое главная дорога по ПДД? Определение
Главная дорога – это статус проезжей части на нерегулируемом перекрестке, в соответствии с которым приоритет для проезда такого перекрестка у транспортных средств, находящихся на главной дороге.
Подчеркнем, что речь идет именно о нерегулируемом перекрестке, т.к. на регулируемом приоритет проезда определяется регулировщиком либо светофором. При наличии сигналов регулировщика или светофора другие указатели приоритета (знаки, разметка) не имеют преимущества.
Еще один важный момент. Главная дорога устанавливает приоритет относительно второстепенной. Транспортные средства (ТС), двигающиеся по равнозначным дорогам, должны пересекать перекресток на основании других правил дорожного движения.
Как определяется главная дорога?
Способы определения указаны в п.1.2 ПДД РФ. Согласно ему, главная дорога определяется:
- Дорожным покрытием. Твердое покрытие делает дорогу главной относительно грунтовой. Причем наличие твердого покрытия только перед выездом на перекресток, не выводит грунтовку из статуса второстепенной.
- Выездом с прилегающей территории. Все такие выезды, если не указано обратного, являются второстепенными дорогами, соответственно, пересекающиеся с ними — главные.
- Дорожными знаками. Об этом поговорим далее более подробно.
Из сказанного вытекает, что в первых двух случаях наличие знаков не является обязательным, приоритет будет установлен самим типом дорог.
Что означает знак «Главная дорога» и «Конец главной дороги»?
Это особо принципиально в крупных населенных пунктах, где два соседних перекрестка, отстающие друг от друга на небольшое расстояние, могут иметь разное преимущество проезда.
Первый способ
Скажем сразу — для этого способа мы будем использовать символ тильда в виде одной волнистой черты, в то время как в знаке приблизительно черты две. Тем менее, тильду часто используют в качестве символа примерно, так что проблем быть не должно.
Используйте англоязычную раскладку. Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:
Или Shift+Alt:
Или используйте языковую иконку, которая находится на панели задач:
Теперь найдите символ тильды (слева от цифры 1, часто на этой же клавише можно увидеть букву ё).
Однако если нажать на указанную клавишу, вы увидите совсем другой символ, поэтому предварительно нажмите на Shift и, удерживая его, нажмите на клавишу тильда, после чего отпустите Shift.
Что у вас должно получиться:
Ориентируемся на знаки
Чтобы понять, кто ведет главную дорогу, а кто движется по второстепенной, нужно смотреть на указательные знаки.
Издалека не всегда удается понять, что считается главной дорогой на приближающемся перекрестке.
В этой ситуации рекомендуется сбросить скорость, а также подъехать ближе.
Далее ориентируйтесь на наличие возможных знаков. Они помогут, если светофор неисправен, либо отсутствует регулировщик.
Посмотрите, какие знаки стоят на перекрестке. И вспомните курсы вождения. Это базовые знания, которые обязаны быть у всех автомобилистов.
Знак 2.1
Непосредственно указывает на то, какая дорога является главной. Означает «Главная дорога».
Если видите этот знак, то впереди перекресток неравнозначных дорог. Следовательно, вы осуществляете движение по главной. У вас приоритет. Пользуйтесь им правильно.
Знак 2.4
Тоже помогает понять, какая дорогая главная на перекрестке. Не ваша. Ведь этот знак сообщает о том, чтобы вы уступили дорогу. Представлен в виде перевернутого треугольника.
Следовательно, водитель движется по дороге второстепенного значения. Сам путь неравнозначный.
При необходимости в случае с таким знаком придется останавливаться. Это нужно, чтобы уступить путь водителям с приоритетом.
Знак 2.5
Еще один полезный знак. Указывает не то, что двигаться без остановки нельзя.
Тоже признак нахождения на дороге второстепенного значения. Перед стоп-линией потребуется остановиться. Если она есть, конечно же.
При отсутствии линии, остановку нужно сделать перед краем проезжей части. Это позволит оценить обстановку, а также принять верное решение о последующих маневрах.
Уступать нужно транспорту, который движется по стороне с приоритетом. Только после этого разрешается продолжить собственный путь.
Категории дорожных знаков
В России, как и в других странах, принявших Венскую конвенцию о знаках дорожного движения, все дорожные указатели по классификации разделены на 8 категорий.
1. Предупреждающие
Назначение предупреждающих знаков – информировать водителя о приближении к зоне, которая может представлять опасность для автомобиля, других участников движения или пешеходов. Водитель должен учитывать информацию и принять меры к повышению безопасности движения. Например, снизить скорость, быть готовым к полной остановке или более внимательно смотреть на обочины. Нарушить требования таких знаков нельзя – они лишь информируют водителей, а не несут запрета на совершение какого-либо маневра.
2. Запрещающие

Запрещающие знаки информируют о полном запрете совершения какого-либо маневра – обгона, остановки, поворота, разворота, проезда и т. д. Нарушение требований этих указателей является нарушением ПДД и наказывается штрафом. Также к этой группе относятся знаки, отменяющие ранее наложенный запрет.
Знаки этой группы устанавливаются перед пересечением или перекрестком, а при необходимости – не далее 25 м в населенных пунктах и не более 50 м – за их пределами. Действие запрета прекращается после соответствующего знака или перекрестка.
3. Знаки приоритета
Используются для определения очередности проезда нерегулируемых светофором пересечений, перекрестков и участков дороги с недостаточной шириной полотна. Среди них – классические указатели «Уступите дорогу», «Главная дорога» и др.
4. Предписывающие

Предписывающие указывают на обязательность выполнения какого-либо маневра – поворота или движения прямо. Невыполнение предписания считается нарушением ПДД и наказывается штрафом.
Также подобными знаками обозначаются велосипедные и пешеходные дорожки. Продолжить движение в этом направлении можно только на велосипеде или пешком.
Обычно предписывающие знаки имеют форму окружности с синим цветом фона. Исключением являются «Направление движения ТС с опасными грузами», которые имеют форму прямоугольника.
5. Знаки особых предписаний
Регулируют ввод или отмену особых режимов движения. По своему значению они соединяют в себе функции разрешительных и информационных указателей, одновременно информируя участников движения о вводе особого режима передвижения и указывая на разрешение какого-либо действия. В эту группу входят знаки, обозначающие автомагистраль, пешеходный переход, остановки общественного транспорта, жилые, велосипедные и пешеходные зоны, начало и конец населенного пункта и т. д.
6. Информационные
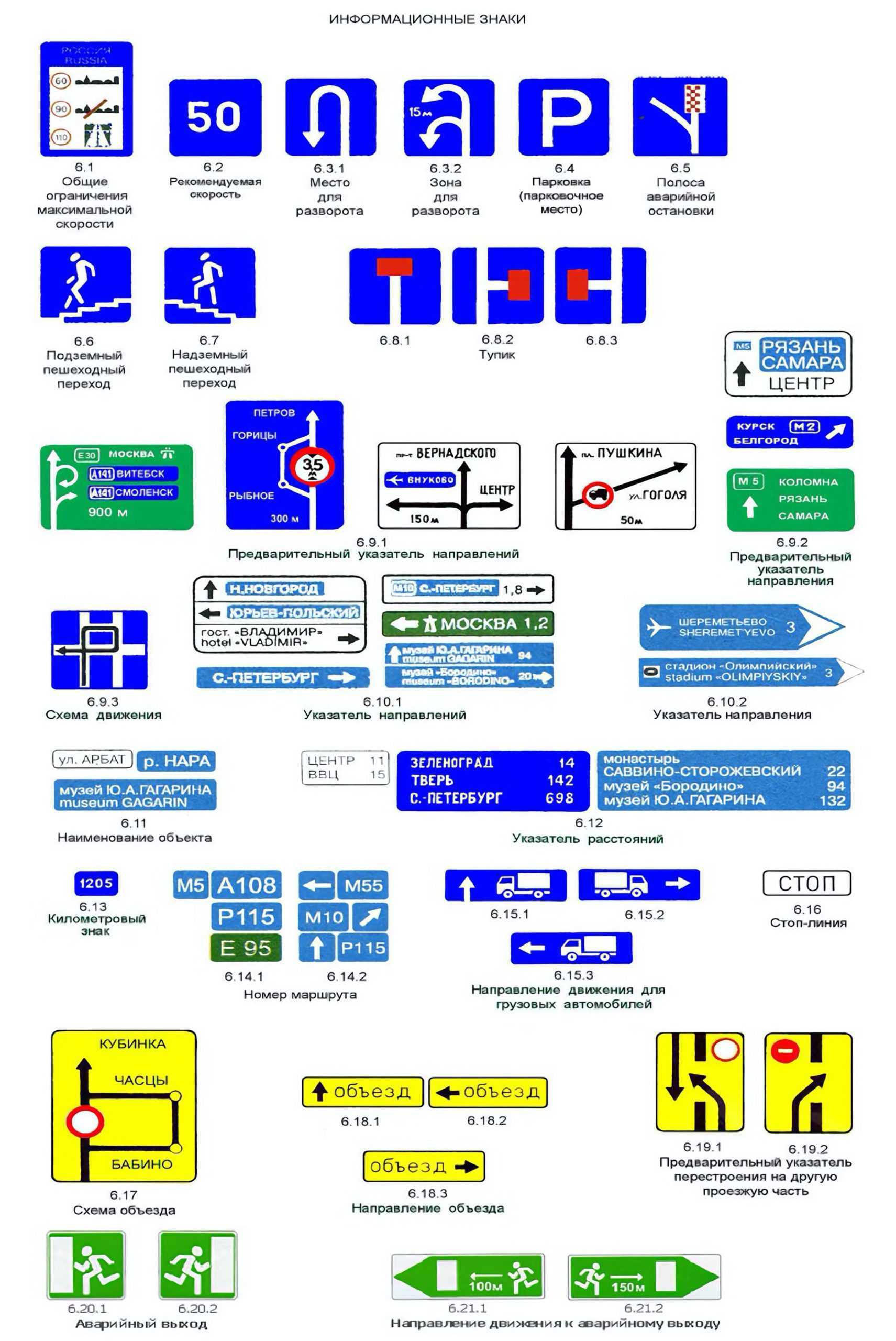
Информационные знаки извещают участников движения о месторасположении населенных пунктов, а также о вводе обязательных или рекомендуемых режимов движения. Знаками этого типа водители и пешеходы информируются о местонахождении пешеходных переходов, расположении улиц, городов и сельских поселений, остановок, рек, музеев, гостиниц и т. д.
7. Знаки сервиса

Знаки сервиса играют исключительно информационную роль и не несут предписаний для участников движения. Их функция – информирование водителей или пешеходов о расположении сервисных объектов – больниц, АЗС, телефонных аппаратов, моек, станций ТО, мест отдыха и т. д.
8. Знаки дополнительной информацией (таблички)
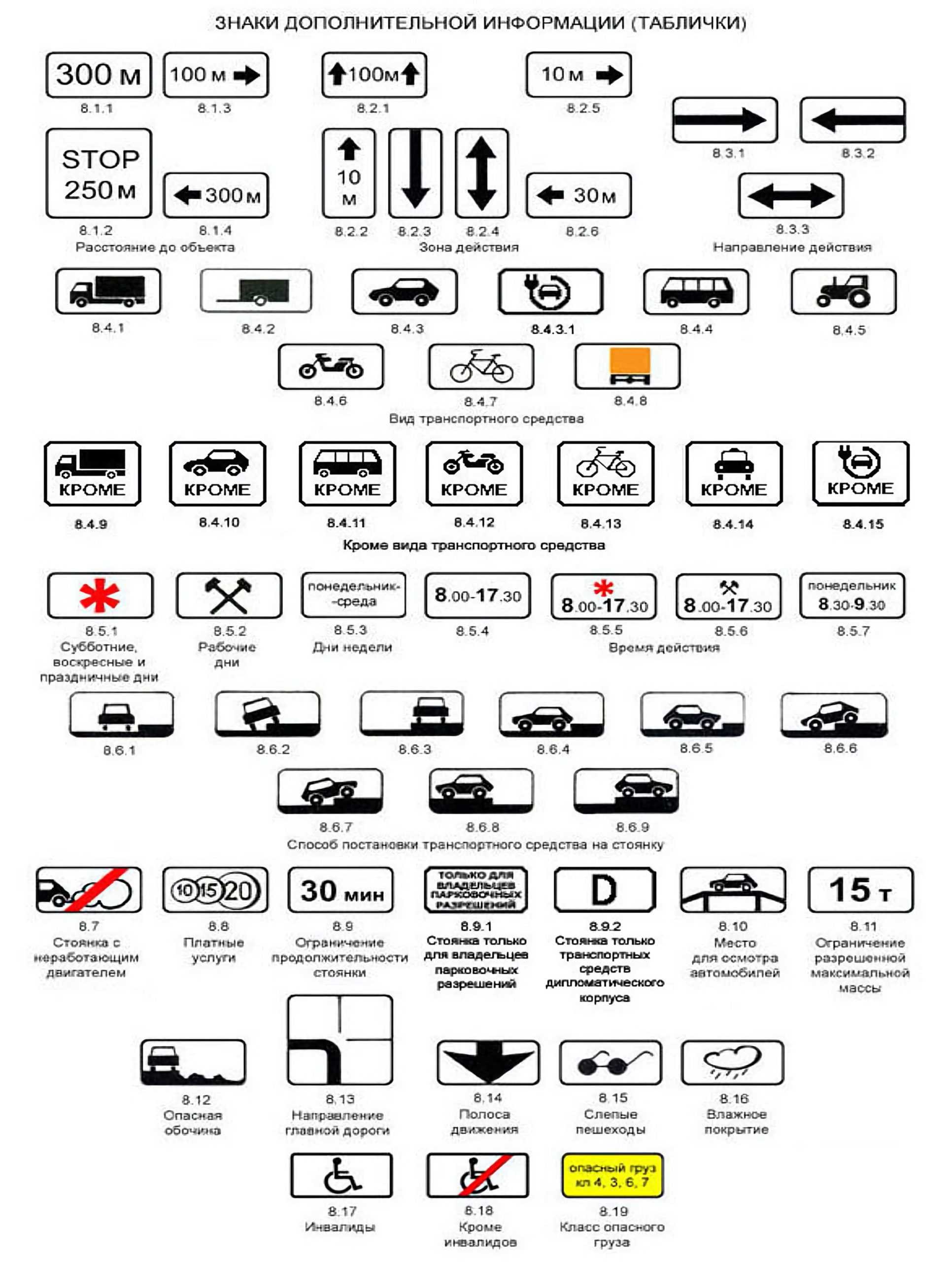
Используются вместе с основным знаком. Назначение табличек – ограничение действия либо уточнение основного дорожного знака. Также таблички могут содержать дополнительную информацию, важную для участников движения.
Таблички выполнены в виде белого прямоугольника, изредка – квадрата. Изображения или надписи на таблички наносятся черным цветом. В подавляющем большинстве случаев указатели дополнительной информации располагаются под основным знаком. Чтобы не перегружать водителя информацией, допускается одновременное использование не более двух табличек вместе с основным указателем.
Когда знаков не видно
Если с вашей стороны дорожные знаки отсутствуют, то следует обязательно сбросить скорость.
Внимательно смотрите по сторонам. Видите знаки с других сторон перекрестка?
Часто их дублируют по левой стороне. Либо подвешивают над дорогой, а не устанавливают сбоку на столбиках.
Причем в некоторых ситуациях устанавливают так, что заметить их невозможно. Распространенной помехой становятся кусты, а также ветки деревьев. Коммунальные службы явно недоработали. И знаки приоритета скрыты в ветвях.
Плохо лишь то, что сей факт вряд ли освободит от ответственности за нарушение правил пересечения перекрестка. Так что будьте внимательными. Смотрите по сторонам.
Если со своей стороны знаков не увидели, тогда присмотритесь к их возможному размещению с других сторон приближающегося перекрестка.
Узнать знаки с обратной стороны не сложно:
- главную дорогу представляют в виде ромба;
- уступать дорогу нужно на перевернутый треугольник;
- двигаться без остановки нельзя, если это восьмигранник.
Увидев на одном из углов перекрестка один из представленных знаков, водитель может правильно оценить ситуацию, а также принять решение о последующих маневрах.
Покрытие в помощь
Другая ситуация, где главная дорога — как определить без знаков.
В такой ситуации есть смысл оценить дорожное покрытие.
Больше актуально за пределами населенных пунктов. Тут также возможны перекрестки, на которых знаки приоритета не устанавливаются.
Есть простое решение. Это наличие грунтового покрытия. Там, где грунт пересекается с асфальтом, все элементарно. Грунт — второстепенный участок, а асфальт — приоритетный, то есть главный.
Да, за определенное количество метров со стороны грунта также может наноситься асфальт. Но лишь для эстетики. Наличие кусочка асфальта на грунте при пересечении перекрестка не делает обе дороги равнозначными. Следовательно, водитель, выезжающий с грунта, должен уступать и пропускать тех, кто движется по асфальтированному покрытию.

































